Nosná kapacita prostředí: Porovnání verzí
Bez shrnutí editace |
Bez shrnutí editace |
||
| Řádek 6: | Řádek 6: | ||
Jako příklad si můžeme představit množení bakterií při kultivačních procesech, kdy se bakterie množí dělením. Z jednoho jedince tedy vzniknou dva, kteří se určité době opět dělí čím vznikají čtyři jedinci z nich osm jedinců atd. | Jako příklad si můžeme představit množení bakterií při kultivačních procesech, kdy se bakterie množí dělením. Z jednoho jedince tedy vzniknou dva, kteří se určité době opět dělí čím vznikají čtyři jedinci z nich osm jedinců atd. | ||
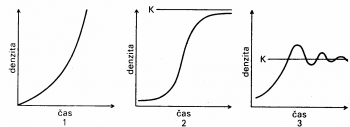
Tento růst je zapisován rovnicí, a graficky znázorňován (obr.1, čas 1): | Tento růst je zapisován rovnicí, a graficky znázorňován (obr.1, čas 1): | ||
[[Soubor:Vzor1.pgn]] | |||
*r – specifická růstová rychlost | *r – specifická růstová rychlost | ||
*N – počet jedinců | *N – počet jedinců | ||
Verze z 10. 1. 2009, 20:11
Nosná kapacita prostředí
Definice: Je maximální velikost populace, která může existovat na daném území neomezeně dlouho, aniž by narušila jeho produkční kapacitu.
Prostředí má omezené zdroje limitující růst populací. Značíme je jako hodnotu K– nosná kapacita prostředí. Růst ideální populace je představován exponenciální řadou. Za ideální populaci se považuje populace s rovnocenností jedinců v populaci, s konstantní specifickou růstovou rychlostí a konstantní nosnou kapacitou prostředí. Počet jedinců populace tedy roste geometrickou řadou. Jako příklad si můžeme představit množení bakterií při kultivačních procesech, kdy se bakterie množí dělením. Z jednoho jedince tedy vzniknou dva, kteří se určité době opět dělí čím vznikají čtyři jedinci z nich osm jedinců atd. Tento růst je zapisován rovnicí, a graficky znázorňován (obr.1, čas 1): Soubor:Vzor1.pgn
- r – specifická růstová rychlost
- N – počet jedinců
S limitujícími faktory prostředí se však exponenciální křivka růstu populace mění na sigmoidní- tzv. S-křivku(logistickou) navrženou Pierrem Francoisem Verhulstem
pro prognózu růstu počtu obyvatel Belgie. To znamená, že se populační růst zastavuje díky vnitrodruhové konkurencí o limitující zdroje při určitém množství a hustotě jedinců na daném území- velikost populace se po dostatečně dlouhém čase ustálí na hodnotě K. Protože vnitřní míra růstu populace i nosná kapacita prostředí jsou druhově/populačně specifické, jeden druh/populace může využívat zdroje v prostředí rozdílně oproti jinému. Je-li populace malá, neprojevuje se u ní vnitrodruhová konkurence a koeficient r je velký. S růstem populace roste také vliv vnitrodruhové konkurence a koeficient r se zmenšuje. Překročí-li velikost populace kritickou hodnotu K, bude koeficient r záporný. Limitujícími faktory pro růst populací může být např.: dostupnost vody, potravy, salinita půdy nebo vody, velikost insolace, velikost teritoria, nevhodné hnízdní stanoviště nebo jejich nedostatek atd..
a toto zpomalení růstu se ho/jí nemusí týkat.
Jako příklad si opět můžeme představit kultivaci bakterií po uplynutíčasového úseku, kdy již bakterie plně vyplnily kultivační prostor. Bakterie si navzájem začínají konkurovat v boji o prostor, snižuje se rychlost množení, naopak mortalita vzrůstá až na úroveň, kdy je populační růst roven nule a velikost populace se stává konstantní. Tento děj je znázorňován logistickou křivkou. Matematicky je vyjádřen modelovou rovnicí a graficky (obr.1, čas 2):
dN/dt = r N (K–N)/K
K – nosná kapacita prostředí r – specifická růstová rychlost N – počet jedinců
Jelikož však velikost populace v běžných přírodních ekosystémech nereaguje ihned, ale s určitým zpožděním, dochází tak k překročení nosné kapacity prostředí. Tento jev se nazývá zpoždění růstové odpovědi populace. Populace tak překročí kritickou hodnotu K, vnitrodruhová konkurence vzroste. Ta má v budoucnosti za následek zvýšení mortality a velikost populace klene pod hodnotu K. Následně opět, z důvodů možnosti růstu populace rychle roste a opět překračuje hodnotu K. Takto populace se zpožděním reaguje a její velikost stále kolísá kolem hodnoty K. (obr.1, čas 3)
Jako příklad si zde může pro zjednodušení představit vztah predátora a kořisti. Pokud je dostatek kořisti, populace predátora vrůstá až do doby, kdy je přesáhne hodnotu K, kdy je kořist přelovena. Nastává okamžik kdy není pro predátora dostatek kořisti, snižuje se velikost natality, mortalita stoupá a počet jedinců opět klesá pod kritickou hodnotu K. Ve chvíli kdy je počet predátora malý, obnovuje se opět velikost populace kořisti. Na toto zvýšení potravní nabídky bude opět predátor se zpožděním reagovat zvětšením populace.

Literatura: Begon M., Harper l. J., Townsend C.R.: Ekologie- jedinci, populace a společenstva, Vydavatelství Univerzity Palackého Olomouc, 1997, s.950) http://etext.czu.cz/img/skripta/68/042_061-1.pdf http://botany.natur.cuni.cz/EkologieRostlin/StrukturaPopulací.ppt
Zdroje
Begon M., Harper l. J., Townsend C.R.: Ekologie- jedinci, populace a společenstva, Vydavatelství Univerzity Palackého Olomouc, 1997, s.950)
Externí odkazy
*EnglWiki